CRITICAL APPRAISAL OF THERAPY PAPER

The quality of clinical trials may be defined as the confidence in the design, conduct, report, and analysis that restrict bias in the comparison of interventions. Critical appraisal of therapy paper is achieved by answering 3 questions:

1. Are the results of the trial valid?
2. How large and precise are the treatment effect?
3. Will the results help me in caring for my patient?

ASSESSMENT OF INTERNAL VALIDITY

This is a crucial step before starting to use the results of a study. To assess the validity means to ask if the findings are true and accurate. It implies that the study is designed well and rigorously conducted to reduce potential bias . One should actively look at the study methodology to assess what was planned and the results ensure that it was actually done. It is common to find a study described as being randomized and upon careful assessment, is found to have poor randomization process. The following RCT components have to be critically evaluated to ensure validity:

1. Randomization
2. Concealed allocation
3. Balanced groups
4. Blinding
5. Equal treatment
6. Compliance
7. Complete follow up
8. Intention to treat analysis

1. Randomization
The patient distribution (allocation) has two steps: the first step is generation of randomization list, which is most often performed by computer programs; and, the second step is execution of allocation by concealment. Randomization is a process by which each subject has 50% chance to be distributed to the intervention or the control group. By randomization, the prognostic factors are distributed equally, which results in two balanced groups. The balance of distribution includes both the known (age, gender, co-morbidities) and the unknown prognostic factors (hereditary and genetic). Randomization protects against selection bias.

2. Concealed allocation
This means that neither the research team nor the patient should know to which group the next patient will be allocated to. If the next assignment is known, enrollment of certain patients may be prevented or delayed to ensure that they receive the treatment believed to be superior. Concealed allocation is based on the sequence generated randomization list. Adequate randomization requires that the allocation of the next patient be unpredictable. Therefore, randomization list must be kept and managed by somebody who is not part of the study (i.e., neither the research team nor the subject). This may be translated by one of two methods:

Remote telephone call can be made especially in multicenter trials. Enrolment of eligible subjects through a telephone call from the center that controls the randomization list will automatically get response and indicate the distribution arm (e.g., A or B).

A second method is by sequentially numbering sealed-opaque envelopes with the distribution (e.g., A or B) on a small piece of paper inside it. But previous evidence demonstrated that envelopes may be trans-illuminated. However, it is still debatable whether sealed envelopes truly provide adequate allocation concealment.

3. Balanced Groups
If the randomization process worked (that is, achieved comparable groups) the groups should be similar. The more similar the groups, the better it is. There may be some indication of whether differences between groups are statistically significant (i.e., p values). The Results should have a table of "Baseline Characteristics," which compares the randomized groups on a number of variables that could affect the outcome (i.e., age, risk factors, etc.).

4. Blinding (Masking)
In RCT, the term "blinding" refers to keeping participants, health-care providers, data collectors, outcome assessors, and/or data analysts unaware of the assigned intervention. The purpose of blinding is to prevent bias associated with patients' and investigators' expectations.18 Blinding usually reduces outcome assessment bias, improves compliance, and reduces drop-out and co-intervention. Blinding also protects against performance bias (i.e., systematic differences in the care provided to the participants in the comparison groups other than the intervention under investigation). Ideally, to minimize bias, both the participant and the investigator are kept blind to (ignorant of) the random assignment. The definition of single-, double-, and triple-blinding varies. Investigators should implement the greatest level of blinding that is feasible. If possible, the following level of blinding should be achieved:

• The patient: to avoid placebo effect and contamination;
• Clinicians: to prevent co-intervention;
• Nurses: to prevent co-intervention;
• Data collectors: to prevent bias in data collection;
• Outcome assessors: to prevent detection bias;
• Data analyst: to prevent bias related to decision about data analysis;
• Any other personnel who are dealing with patients and who are part of the research team (i.e., pharmacists, dietician, health educator, physiotherapist, etc).
If interventions are compared with no intervention, an identical placebo may be used. The compared interventions must be identical in taste, smell, appearance, and mode of administration.

5. Equal Treatment
Investigator should ensure that apart from the intervention the patients in the different groups should be treated the same in terms of additional treatments or tests. The results should include a section for the follow-up schedule and permit for additional treatments or contamination. Contamination occurs when either the intervention group or the control group receives part or all of the other group treatment. For example, in a trial of dietary change, people in the control group might learn about the experimental diet and adopt it themselves. Contamination may reduce the point estimate on the intervention. Two ways are used to reduce the effect of contamination: first, by increasing the sample size; and second, by cluster randomization where no interaction is allowed between intervention and control group (e.g., schools and PHCs randomization). Co-intervention implies additional Interventions other than the treatment or procedure defined per protocol under study that is applied differently to the treatment and control groups. Co-intervention is a serious problem when double blinding is absent or when the use of very effective non-study treatment is permitted. Example is the multiple sclerosis trial; the new drug may appear to be more effective at the end of the trial if patients allocated to the new drug received physiotherapy earlier and more intensively than patients allocated to placebo.

6. Compliance
Usually, treatment efficacy is based on the compliant subjects. Non-compliance with treatment regimen is a common protocol violation in RCT. It compromises the desired rigor of the trial. Non-compliance can seriously decrease study power resulting in widely varying estimates of the sample size required for a study. Thus, non-compliance is a significant issue to be considered when appraising trials involving long-term therapies.

7. Follow-up
Dropout in RCT is common and threatens the validity of results, as completers may differ from people who drop out. Lost to follow up includes all patients whose status is not known at the end of the study, such as:

• Complete non follow-up - left study
• Incomplete follow up - missed some visits
• Data was not collected or missing
• Data was corrupted or not analyzed

Rubin, and Donald (1976), classified dropout as:
a. Administrative: If patients withdraw from a study for a reason unrelated to their disease or treatment (for example, because they have moved overseas) their data are probably missing completely at random, because of no systematic differences between them and the patients who remained in the study.
b. Clinical: If patients withdraw from the study for reasons related to their disease or treatment (e.g., progression or toxicity); their quality of life measures would have been worse than those of patients who remained in the study. Some authors considered loss to follow-up of 5% or lower, is usually of little concern; whereas, a loss of 20% or greater means that readers should be concerned about the possibility of bias. Losses between 5% and 20% may still be a source of bias.
c. If investigators stop following patients who do not adhere to the study protocol, they will be unaware if those patients suffered the target outcome. Investigators often include patients lost to follow-up in the denominators in calculating estimates of effect. This approach assumes that none of those lost to follow-up suffered the target outcome. Making this unlikely assumption opens the door to a misleading presentation of study results. Alternative strategies are available that impute outcomes to those lost to follow up. Some of these strategies include:

i. Attempt to follow up all randomized participants: Following up participants who withdraw from randomized treatment can be difficult but is important because they may differ systematically from those who remain on treatment. A trial that does not attempt to follow participants after treatment withdrawal cannot claim to follow the intention to treat principle
ii. Perform plausible main analysis: The main analysis should be chosen to be valid under a plausible assumption about the missing data. For example, in a hypothetical trial, consider in 100 participants, 10 had dropped-out at 6 months and the rest (90 participants) are followed at least to 12 months. The outcomes at 6 months are similar in those dropped out and the completers. In case the reason of drop-out of the 10 participants is administrative (not treatment or disease related), it's logical to consider that the outcome rate remains similar in both groups at 12 months.
iii. Perform sensitivity analyses: For a bad outcome, apply the worst case scenario for lost to follow up at the intervention arm and best case scenario for lost-to-follow up at the control arm.

8. Intention to Treat Principle (ITT)
There is ongoing debate on which participants should be analyzed. Per protocol analysis (i.e., efficacy analysis, explanatory analysis, or analysis by treatment administered) describes the outcomes of the participants who adhered to the research protocol. Although investigators can use information from such an analysis to estimate the intervention's efficacy in those who actually received it in the intended intensity or dose for the intended interval; this estimate is likely to be seriously flawed. The problem arises because the reasons for non-adherence to the protocol may be related to prognosis. ITT analysis includes all randomized patients in the groups to which they were randomly assigned and their outcomes, regardless of their adherence with the entry criteria, regardless of the treatment they actually received, and regardless of subsequent withdrawal from treatment or deviation from the protocol. In other words, ITT analysis includes every subject who is randomized according to randomized treatment assignment. It ignores non-compliance, protocol deviations, withdrawal, and anything that happens after randomization.

Excluding non-compliant or deviators may overestimate the efficacy of intervention by ignoring the harm that resulted in non-compliance and deviation. ITT analysis reflects the practical clinical scenario because it admits non-compliance and protocol deviations. ITT analysis maintains prognostic balance generated from the original random treatment allocation. It gives an unbiased estimate of treatment effect. If non-compliant subjects and dropouts are excluded from the final analysis, it might create important prognostic differences among treatment groups. Moreover, subjects may be non-compliant or may drop out from the study due to their response to treatment. ITT analysis preserves the sample size because if non-compliant subjects and dropouts are excluded from the final analysis, it might significantly reduce the sample size, leading to reduced statistical power. The drawback of ITT analysis is that, it is too cautious and more susceptible to type II error (cannot reject null hypothesis in the setting of effective treatment); and it is less likely to show a positive treatment effect.

A full application of the ITT analysis is only possible when complete outcome data are available for all randomized subjects. In other words, ITT analysis cannot minimize bias introduced by loss to follow-up, that is, patients whose outcome status is unknown.

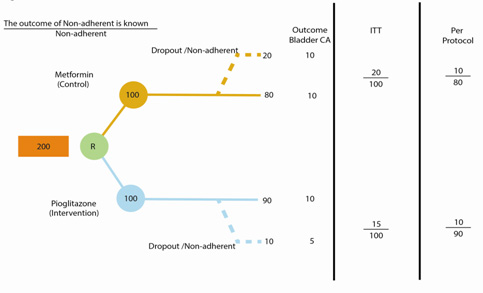
ASSESSMENT OF TREATMENT EFFECT

Most often, results are presented as dichotomous outcomes (yes or no outcomes that happen or don't happen) and can include such outcomes as cancer recurrence, myocardial infarction, and death. Two types of measure effects are:
1. How large was the treatment effect (magnitude)?
- Relative effects (Relative Risk [RR] and Relative Risk Reduction [RRR])
- Absolute effects (Absolute Risk Reduction [ARR] and number needed to treat [NNT])
2. How precise was the estimate of the treatment effects?
- 95% confidence interval (CI)

1. Relative Risk
The relative risk (RR) tells us how many times more likely it is that an event will occur in the treatment group relative to the control group. An RR of 1 means that there is no difference between the two groups thus, the treatment had no effect. An RR<1 means that the treatment decreases the risk of the outcome. An RR>1 means that the treatment increased the risk of the outcome. RR is a ratio of probabilities. It compares the incidence or risk of an event among those with a specific exposure with those who were not exposed (e.g., myocardial infarctions in those who smoke cigarettes compared with those who do not). RR is based upon the incidence of an event given that we already know the study participants' exposure status. It is only appropriate, therefore, to use RR for prospective cohort studies.

Consider this example of an RCT using Voglibose by Impaired Fasting Glucose patients to prevent progression to Type-2 diabetes mellitus. Subjects treated with voglibose had a significantly lower risk for progression to type-2 diabetes than those in placebo group (Table 1).

Table 1: Voglibose 50/897 vs Placebo 106/881


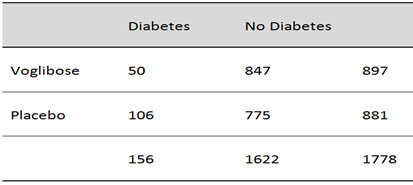
Table 1 shows the dataset of patients treated with either Voglibose or placebo. This example can be used to calculate the treatment effect (RR, RRR, ARR and NNT).

The risk (incidence) of diabetes among those treated with Voglibose may be calculated using the experimental event rate (EER) or Risk in the treatment group (Rt):
EER = 50 ÷ 897 = 0.0557

The risk (incidence) of diabetes among Control group is equal to control event rate (CER) or Risk in control group (Rc):
CER = 106 ÷ 881 = 0.1203

From these two risks, the RR is calculated as:
RR = EER ÷ CER = 0.0557 ÷ 0.1203 = 0.46

A RR of 0.46 means that the probability of voglibose users to develop type-2 diabetes is 0.46 times that of the controls. This is called also Risk Ratio and Risk Remaining. Risk Remaining indicates the risk occurrence in spite of using the intervention.

2. Relative Risk Reduction
The relative risk reduction (RRR) is a complement of RR and is probably the most commonly reported measure of treatment effects. It tells us the reduction in the rate of the outcome in the treatment group relative to that in the control group (Figure 2).


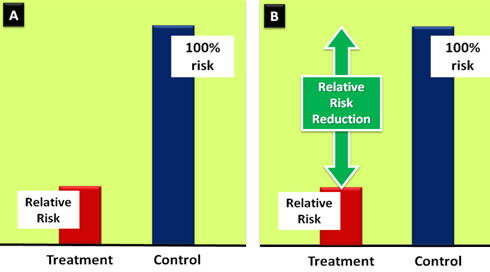
Figure 2: Graphical depiction of the relationship between the RR and RRR

RRR = 1 - RR
RRR = 1 - 0.46 = 0.54 = 54%

The treatment reduced the risk of diabetes by 54% relative to that occurring in the control group.

3. Absolute Risk Reduction
The absolute risk reduction (ARR) tells the absolute difference in the rates of events between the two groups and gives an indication of the baseline risk and treatment effect. An ARR of 0 means that there is no difference between the two groups thus, the treatment had no effect. It is calculated as the difference in the risk of the outcome in the control group compared to the risk of the outcome in the treatment group. This is also known as the risk difference:
ARR = CER - EER
ARR = 12.03% - 5.57% = 6.46%

4. Number Needed to Treat
The number needed to treat (NNT) is the number of patients you need to treat to prevent one additional bad outcome (e.g., death, stroke, etc.). For example, if a drug has an NNT of 10, it means you have to treat 10 people with the drug to prevent one additional bad outcome. The duration of the treatment has to be incorporated in the assessment of the NNT. To calculate the NNT, you need to know the ARR since the NNT is the inverse of the ARR:

NNT = 1 ÷ ARR
NNT = 1 ÷ 6.46 = 16

Therefore, in this example, 16 subjects have to be treated with voglibose for an average of 4 years to prevent one case of type-2 diabetes.

RRR does not take into account the individuals' risk of achieving the intended outcome without the intervention. Therefore, they do not give a true reflection of how much benefit the individual would derive from the intervention, as they cannot discriminate between small and large treatment effects. They usually tend to overemphasize the benefits of an intervention and, for this reason, drug companies and the popular media love RR measures! ARR measures overcome these drawbacks because they reflect the baseline risk and are better at discriminating between small and large treatment effects.

Using the data from Table 1, you will recall that we calculated the ARR as 6.46% and the relative risk reduction as 54%. Fifty four percent reductions in risk feels more impressive than 6.46%.

Consider an example of disease with rare event rate (e.g., 2 in 10,000). The proposed treatment reduced the event rate to 1 per 10,000:
The CER is 2/10,000=0.0002
The EER is 1/10,000 =0.0001
The relative risk is 0.0001/0.0002=0.5

The RRR at 50% is obvious that the 50% reduction may not be as important as it looks. On further analyzing the ARR 0.0002-0.0001=0.0001, has very tiny small benefit. How small the treatment effect is, it becomes even more obvious after calculating the NNT:
NNT = 1/AAR = 1/0.0001=10,000

Thus, 10,000 patients must be treated to prevent one event.

PRECISION OF THE ESTIMATES OF TREATMENT EFFECT

The true risk of the outcome in the population is not known and the best we can do is estimate the true risk based on the sample of patients in the trial. This estimate is called the point estimate. We can gauge how close this estimate is to the true value by looking at the confidence intervals (CI) for each estimate. If the CI is fairly narrow then we can be confident that our point estimate is a precise reflection of the population value. The CI also provides us with information about the statistical significance of the result. If the value corresponding to no effect falls outside the 95% confidence interval, then the result is statistically significant at the 0.05 level. If the confidence interval includes the value corresponding to no effect, then the results are not statistically significant.

APPLICATION OF STUDY RESULTS TO MY PATIENT

One should consider focusing on issues related to intervention, patient, potential harm, and patient preference [IPPP]. The first issue to address is how confident you are that you can apply the results to a particular patient or patients in your practice. If the patient would have been enrolled in the study had he/she been eligible? Patient is eligible if he/she meets all the inclusion criteria, and does not violate any of the exclusion criteria. In this case, there is doubt that the results are applicable. If this is not the case, judgment is required. A better approach than rigidly applying the study's inclusion and exclusion criteria is to ask whether there is some compelling reason why the results should be applied to the patient. A compelling reason usually would not be found, and most often you can generalize the results to your patient with confidence.

If the article's results are generalizable to your patient and its outcomes are important, the next question concerns whether the probable treatment benefits are worth the effort that you and your patient must put into the enterprise. For any RCT, safety issues have to be considered as secondary outcome. A fair balance must exist between the magnitude of benefit and potential harm. As discussed earlier, NNT can tell you the likelihood of benefit. Nevertheless, for each intervention we should also calculate the number needed to harm (NNH), i.e., the number of patients needed to treat before having serious harm. We might not hesitate to treat even as many as 400 patients to save one life if the treatment was cheap, easy to apply, compliant, and safe. In reality, however, treatments usually are expensive and they carry risks.

The patient is an integral part of the management. One of the most common sources of patient dissatisfaction is not feeling properly informed about (and involved in) their treatment. Shared decision-making, where patients are involved as active partners with the clinician in treatment decisions, can be recommended as an effective way to tackle this problem. Though unlikely, a patient may prefer to avoid taking treatment with clear benefit and small harm, merely due to cultural or religious reasons.

CONCLUSION

On concluding this chapter, we hope that you are developing a sense of how to use evidence- based medicine module to appraise therapy article.(40, 41) Once you find an article relevant to the therapeutic issue, be sure to assess the quality of the evidence. If the quality of the evidence is poor, any subsequent inference (and the clinical decision it generates) will be weakened. If the quality of the evidence is adequate, determine the range within which the true treatment effect likely falls.

Then, consider the extent to which the results are generalizable to the patient at hand, and whether the outcomes that have been measured are important. If the generalizability is in doubt or the importance of the outcomes questionable, support for a treatment recommendation will be weakened. Finally, by taking into account the patient's risk of adverse events, assess the feasibility of the intervention. This involves a balance sheet looking at the probability of benefit; and the associated costs and risks. Different aspects of the balance sheet help to guide your treatment decision.

REFERENCES

1. Kjaergard LL, Villumsen J, and Gluud C. Reported methodologic quality and discrepancies between large and small randomized trials in meta-analyses. Ann Intern Med. 2001;135(11):982-989.
2. Koh HK, et. al. A proposed 'health literate care model' would constitute a systems approach to improving patients' engagement in care. Health Aff (Millwood). 2013;32(2): 357-367.
3. Sibbald B. and Roland M. Understanding controlled trials. Why are randomised controlled trials important? BMJ. 1998;316(7126):201.
4. Yusuf S, Collins R, and Peto R. Why do we need some large, simple randomized trials? Stat Med. 1984;3(4): 409-422.
5. Price DD, Finniss DG, and Benedetti F. A comprehensive review of the placebo effect: recent advances and current thought. Annu Rev Psychol. 2008;59: 565-590.
6. Rajagopal S. The placebo effect. The Psychiatrist. 2006;30: 185-188. Psychiatric Bulletin (2006)30: 185-188doi: 10.1192/pb.30.5.185
7. Fernald DH, Coombs L, DeAlleaume L, West D, and Parnes B. An Assessment of the Hawthorne Effect in Practice-based Research. J Am Board Fam Med. 2012;25(1):83-86.
8. Oxman AD, Guyatt GH, Singer J, Goldsmith CH, Hutchison BG, Milner RA, and Streiner DL. Agreement among reviewers of review articles. J Clin Epidemiol. 1991;44(1):91-98.
9. Schulz KF, Chalmers I, Hayes RJ, and Altman DG. Empirical evidence of bias. Dimensions of methodological quality associated with estimates of treatment effects in controlled trials. JAMA. 1995;273(5):408-412.
10. Klein MC, Kaczorowski J, Robbins JM, Gauthier RJ, Jorgensen SH, and Joshi AK. Physicians' beliefs and behaviour during a randomized controlled trial of episiotomy: consequences for women in their care. CMAJ, 1995;153(6):769-779.
11. Kunz R, Vist G, and Oxman AD. Randomisation to protect against selection bias in healthcare trials. Cochrane Database Syst Rev. 2007;2:MR000012.
12. Wood L, et. al. Empirical evidence of bias in treatment effect estimates in controlled trials with different interventions and outcomes: meta-epidemiological study. BMJ, 2008; 336(7644):601-605.
13. Altman D.G. and Bland JM. Statistics notes. Treatment allocation in controlled trials: why randomise? BMJ. 1999;318(7192):1209.
14. Altman DG and Bland JM. How to randomise. BMJ. 1999;319(7211):703-704.
15. Schulz KF. Subverting randomization in controlled trials. JAMA. 1995;274(18):1456-1458.
16. Swingler GH. and Zwarenstein M. An effectiveness trial of a diagnostic test in a busy outpatients department in a developing country: issues around allocation concealment and envelope randomization. J Clin Epidemiol. 2000;53(7):702-706.
17. Devereaux PJ, et. al. Physician interpretations and textbook definitions of blinding terminology in randomized controlled trials. JAMA. 2001;285(15):2000-2003.
18. Juni P, Altman DG, and Egger M. Systematic reviews in health care: Assessing the quality of controlled clinical trials. BMJ, 2001;323(7303):42-46.
19. Schulz KF and Grimes DA. Blinding in randomised trials: hiding who got what. Lancet. 2002 Feb 23;359(9307):696-700.
20. Torgerson, DJ. Contamination in trials: is cluster randomisation the answer? BMJ, 2001; 322(7282): 355-357.
21. Musahl V. et. al. The pivot shift: a global user guide. Knee Surg Sports Traumatol Arthrosc. 2012;20(4): 724-731.
22. Whitney CW and Dworkin SF. Practical implications of noncompliance in randomized clinical trials for temporomandibular disorders. J Orofac Pain, 1997;11(2): 130-138.
23. Snapinn SM. Jiang Q, and Iglewicz B. Informative noncompliance in endpoint trials. Curr Control Trials Cardiovasc Med. 2004;5(1):5.
24. Rotnitzky A, Lei Q, Sued M, and Robins JM. Improved double-robust estimation in missing data and causal inference models. Biometrika. 2012;99(2):439-456. Inference and missing data. Biometrika 1976. 63: p. 581-92.
25. Bell ML, et. al. Differential dropout and bias in randomised controlled trials: when it matters and when it may not. BMJ. 2013;346:e8668.
26. Dumville JC, Torgerson DJ, and Hewitt CE. Reporting attrition in randomised controlled trials. BMJ. 2006;332(7547):969-971.
27. Fergusson D, et. al. Post-randomisation exclusions: the intention to treat principle and excluding patients from analysis. BMJ. 2002;325(7365): p. 652-654.
28. Montori VM and Guyatt GH. Intention-to-treat principle. CMAJ. 2001;165(10):1339-41.
29.Burzykowski T, Carpenter J, Coens C, Evans D, France L, Kenward M, Lane P, Matcham J, Morgan D, Phillips A, Roger J, Sullivan B, White I, Yu LM; of the PSI Missing Data Expert Group. Pharm Stat. 2010 Oct-Dec;9(4):288-97. doi: 10.1002/pst.391. PMID: 19844946
30. "The prevention and treatment of missing data in clinical trials." National Research Council (US) Panel on Handling Missing Data in Clinical Trials. Washington (DC), US: National Academies Press. 2010. 31. Gupta SK. Intention-to-treat concept: A review. Perspect Clin Res. 2011;2(3): 109-112.
32. Heritier SR, Gebski VJ, and Keech AC. Inclusion of patients in clinical trial analysis: the intention-to-treat principle. Med J Aust. 2003;179(8): 438-440.
33. Newell DJ. Intention-to-treat analysis: implications for quantitative and qualitative research. Int J Epidemiol. 1992;21(5): 837-841.
34. Coronary Drug Project. Influence of adherence to treatment and response of cholesterol on mortality in the Coronary Drug Project. N Engl J Med. 1980;303: 1038-1041.
35. Horwitz R, et.al. Treatment adherence and risk of death after myocardial infarction. Lancet. 1990;336: 542-545.
36. Altman DG. "Clinical Trials." Practical Statistics for Medical Research. CRC Press. 1991.
37. Sommer A. and Zeger SL. On estimating efficacy from clinical trials. Stat Med. 1991;10(1):45-52.
38. Rubin, Donald B. 1976. Inference and missing data. Biometrika 63(3): 581-592. http://nrs.harvard.edu/urn-3:HUL.InstRepos:3408223
39. Hollis S. A graphical sensitivity analysis for clinical trials with non-ignorable missing binary outcome. Stat Med. 2002;21:3823-3384.
40. Mazen Ferwana, Ashraf El Metwally. How to do Systematic Review and Meta-analysis.
Middle East Journal of Family Medicine, October 2015, Volume 13, Issue 7.
41. Mazen Ferwana, Critical Reading of an Article about Causation and Harm, Middle East Journal of Family Medicine, September 2015 , Volume 13, Issue 6